Cosine Contours A Multipurpose Representation for Melodies
Representing shapes of melodies using cosine functions
- collaborators
- John Ashley Burgoyne & Jelle Zuidema
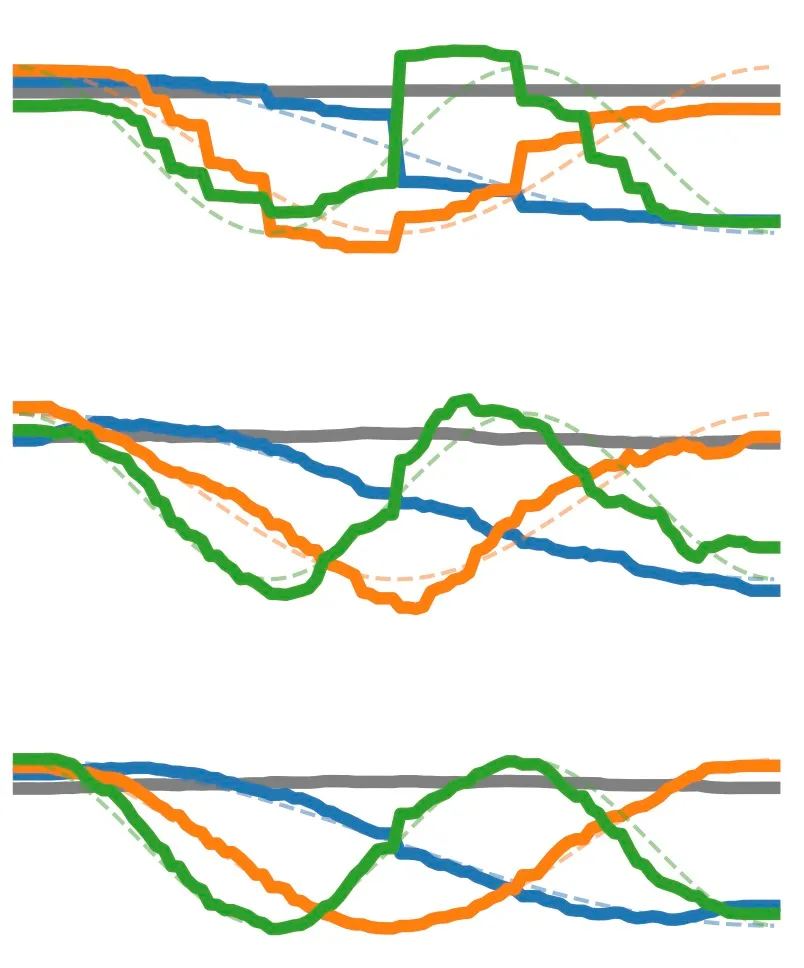
Here’s a funny observation. Suppose you take a lot of melodies, and measure the pitch height at, say, 50 points in time, equally spaced between the start and end of the melody. All your melodies are now sequences of 50 pitches: a 50 dimensional dataset. The principal components of this dataset will probably look like cosine functions.
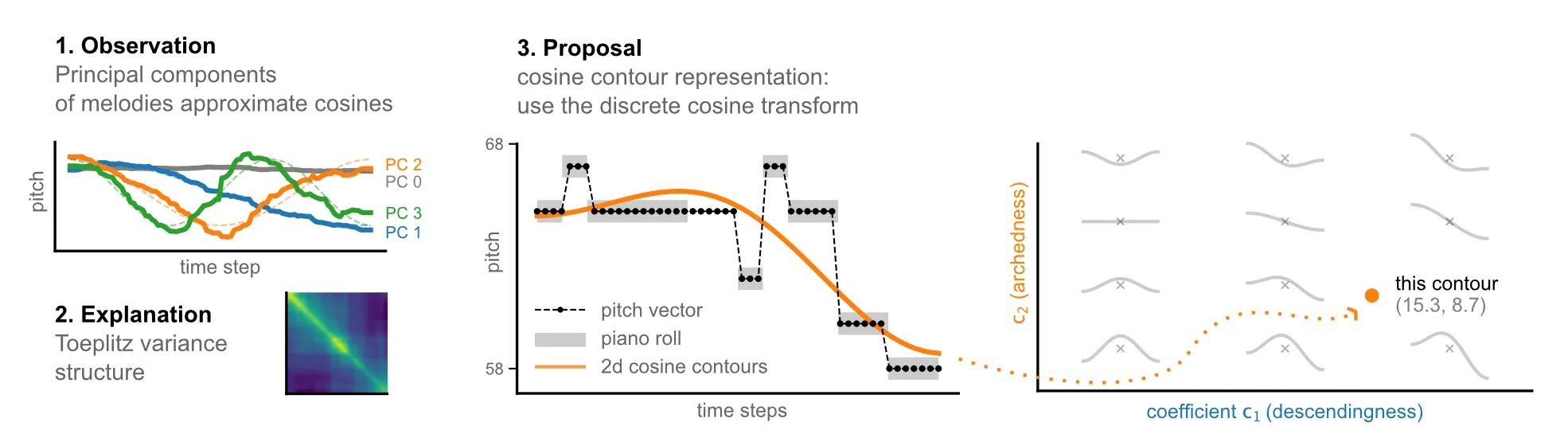
In this paper we demonstrate that the principal components of melodies (from motifs and phrases to complete songs) tend to be cosine-shaped. The same is true for artificial random-walk melodies and this suggests that the cosines are a kind of mathematical artefact. The culprit turns out to be the covariance matrix. This roughly approximates a so called Toeplitz matrix, and such matrices (asymptotically) have sinusoidal eigenvectors: our principal components.
Now suppose want to efficiently describe the contour of melodies, capturing as much of the variability in as few dimensions as possible. A principal component projection would be the best choice, but our observations show that we might as well use cosines instead of the principal components, and use a discrete cosine transform. This leads us to propose cosine contours which are simply the discrete cosine transforms of the melodies (pitch sequences). We present three short case studies to illustrate their practical usefulness.
📖 Paper (supplements) • 🎬 Video • 📜 Poster/slides
Bas Cornelissen, Willem Zuidema, and John Ashley Burgoyne (2021). Cosine Contours: A Multipurpose Representation for Melodies. Proceedings of the 22st International Society for Music Information Retrieval Conference, Online.